U.E Olga Bayone, German Ng

¿Definicion de un logaritmo?

Dado un número real (argumento x), la función logaritmo le asigna el exponente n (o potencia) a la que un número fijo se ha de elevar para obtener dicho argumento. Es la función inversa de b a la potencia n. Esta función se escribe como: n = log_b x, lo que permite obtener n.²

$\log_b x = n\Leftrightarrow\ x = b^n\,$

(esto se lee como: logaritmo en base "b" de "x" es igual a "n"; sí y sólo si "b" elevado a la "n" da por resultado a "x")

La base b tiene que ser positiva y distinta de 1 $(b>0, b \ne 1)\,$ .
x tiene que ser un número positivo $(x>0)\,$ .
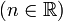n puede ser cualquier número real $(n\in\mathbb{R})\,$ .

Así, en la expresión 10² = 100, el logaritmo de 100 en base 10 es 2, y se escribe como log₁₀ 100 = 2.

¿Identidades Logaritmicas?

Los logaritmos mantienen ciertas identidades aritméticas muy útiles a la hora de realizar cálculos:

El logaritmo de un producto es igual a la suma de los logaritmos de los factores.

$\!\, \log(a b) = \log(a) + \log(b) \,$

El logaritmo de un cociente es igual al logaritmo del numerador menos el logaritmo del denominador.

$\!\, \log(a / b) = \log(a) - \log(b) \,$

El logaritmo de una potencia es igual al producto entre el exponente y el logaritmo de la base de la potencia.

$\!\, \log(a ^ x) = x \log(a) \,$

El logaritmo de una raíz es igual al producto entre la inversa del índice y el logaritmo del radicando.

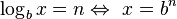
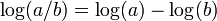
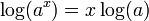
$\!\, \log(\sqrt[x]{y}) = \frac{\log(y)}{x} \,$

En realidad la tercera y cuarta identidad son equivalentes, sin más que hacer:

$\!\, \sqrt[x]{y} = y^\frac{1}{x} \,$

U.E Olga Bayone, German Ng

martes, 8 de noviembre de 2011

Matematica (Logaritmo)