martes, 8 de noviembre de 2011

Matematica (Logaritmo)

¿Definicion de un logaritmo?
Dado un número real (argumento x), la función logaritmo le asigna el exponente n (o potencia) a la que un número fijo se ha de elevar para obtener dicho argumento. Es la función inversa de b a la potencia n. Esta función se escribe como: n = logb x, lo que permite obtener n.2
\log_b x = n\Leftrightarrow\ x = b^n\,
(esto se lee como: logaritmo en base "b" de "x" es igual a "n"; sí y sólo si "b" elevado a la "n" da por resultado a "x")
  • La base b tiene que ser positiva y distinta de 1 (b>0, b \ne 1)\,.
  • x tiene que ser un número positivo (x>0)\,.
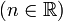  • n puede ser cualquier número real (n\in\mathbb{R})\,.
Así, en la expresión 102 = 100, el logaritmo de 100 en base 10 es 2, y se escribe como log10 100 = 2.

¿Identidades Logaritmicas?

Los logaritmos mantienen ciertas identidades aritméticas muy útiles a la hora de realizar cálculos:
  • El logaritmo de un producto es igual a la suma de los logaritmos de los factores.
\!\, \log(a b) = \log(a) + \log(b) \,
  • El logaritmo de un cociente es igual al logaritmo del numerador menos el logaritmo del denominador.
\!\, \log(a / b) = \log(a) - \log(b) \,
  • El logaritmo de una potencia es igual al producto entre el exponente y el logaritmo de la base de la potencia.
\!\, \log(a ^ x) = x \log(a) \,
  • El logaritmo de una raíz es igual al producto entre la inversa del índice y el logaritmo del radicando.
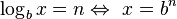
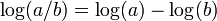
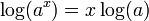
\!\, \log(\sqrt[x]{y}) = \frac{\log(y)}{x} \,
En realidad la tercera y cuarta identidad son equivalentes, sin más que hacer:
\!\, \sqrt[x]{y} = y^\frac{1}{x} \,
Publicado por en

10 comentarios:

Suscribirse a: Enviar comentarios (Atom)